NEMESIS: 1. Tunable phononic crystals and invariant nonlinear materials
This project focuses on understanding and developing mathematical techniques associated with the modelling of phononic crystals, parts of which are "soft" or "compliant". This property generally leads to some aspect of the material behaviour being "tuned" which is normally a useful aspect for applications.
We are also studying what I have termed "invariant" compliant materials, where some property remains fixed even after large deformation. This is an unusual phenomenon but could be extremely useful in practice.
We are also studying what I have termed "invariant" compliant materials, where some property remains fixed even after large deformation. This is an unusual phenomenon but could be extremely useful in practice.
|
Tunable phononics
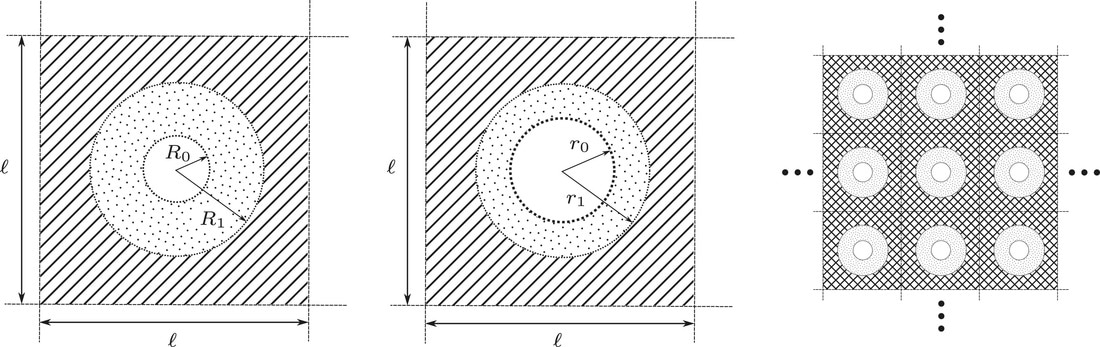
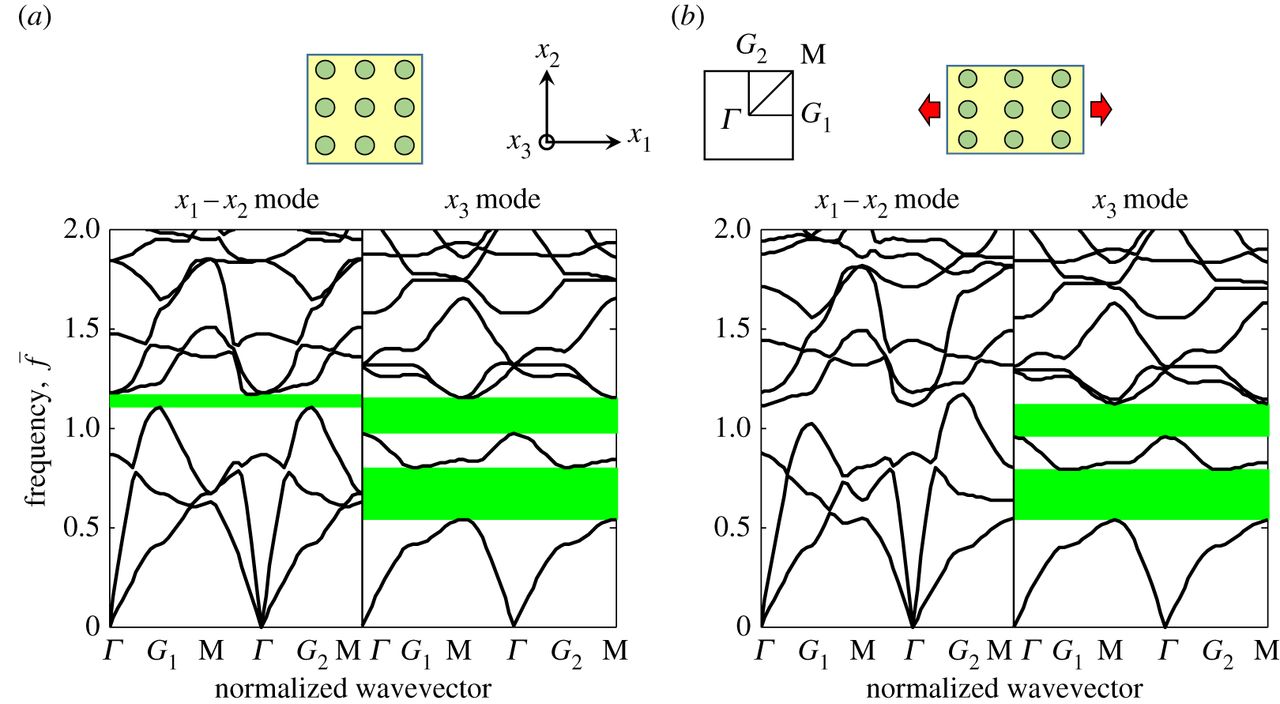
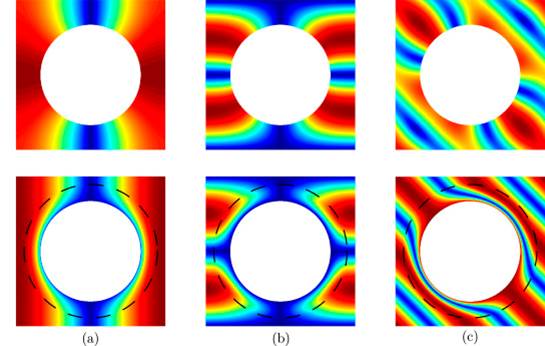
In recent times phononic crystals have been found to be very useful. These are devices fabricated as periodic arrangements of one material embedded in another matrix phase. These materials allow acoustic and elastic waves to be blocked within certain frequency ranges (so-called band gaps). Pre-stress and other external mechanisms have been used to tune such behaviour. In two papers written with my former PhD student Ellis Barnwell we introduced a new phononic crystal with soft internal structure (annular fibres) that are deformable, thus giving rise to tunable behaviour. The structure is illustrated here, where the periodic cell in the initial (left) and deformed (middle) states are shown, together with the phononic crystal itself (right). The first paper appeared in Wave Motion in 2016, focusing on the antiplane elastic (SH) waves. In particular in this paper we introduced the interesting concept of a phononic cloak. This is depicted below. The fibre annulus material is a neo-Hookean nonlinear elastic material and based on the concept of hyperelastic invariance introduced in a paper of mine that appeared in Proceedings A in 2012, we showed that it is possible to pre-stress these fibre annuli radially into a geometrical configuration that would normally render band gaps, but here there are no band gaps whatsoever. |
Soft phononic crystals with deformation-independent band gaps
As indicated by the work described on the left, soft phononic crystals have always been used as mechanisms to modify the band-gap structure of a periodic material. This has been seen as a useful effect, using either nonlinear elastic pre-stress or deformation induced by say electric or magnetic fields for example. A question that has never been asked before is "do soft phononic crystals exist that have a band-gap structure that is invariant to deformation?". One could imagine situations where one wanted the band-gap structure to remain unchanged even after deformation. In a paper in Proceedings A, my postdoc Pu Zhang and I showed that one can use semi-linear and neo-Hookean nonlinear elastic materials to give rise to this effect in fibrous type periodic materials. A neo-Hookean matrix with stiff fibrous inclusions gives rise to deformation-independent band gaps for antiplane elastic (SH) waves, whereas a semi-linear matrix with voids leads to deformation-independent band gaps in the in-plane compressional/shear (P/SV) wave scenario. |
|
The figure above illustrates this concept nicely. The mode shapes are illustrated for a periodic cell of what we term a phononic cloak. The top row shows a stress-free homogeneous host material with cavities of radius R=0.33. The bottom row shows a pre-stressed material with initial radius R=0, axial stretch ζ=2.2,with final deformed radius r=0.33. The material properties of the neo-Hookean annular region are chosen as μ=ζ μ0 (shear modulus) and ρ=ζ ρ0 (density) where μ0 and ρ0 are the shear modulus and density of the matrix. The wavenumbers chosen in (a) and (b) are kx=π, ky=0 whereas in (c) kx=π/2, ky=π/2.
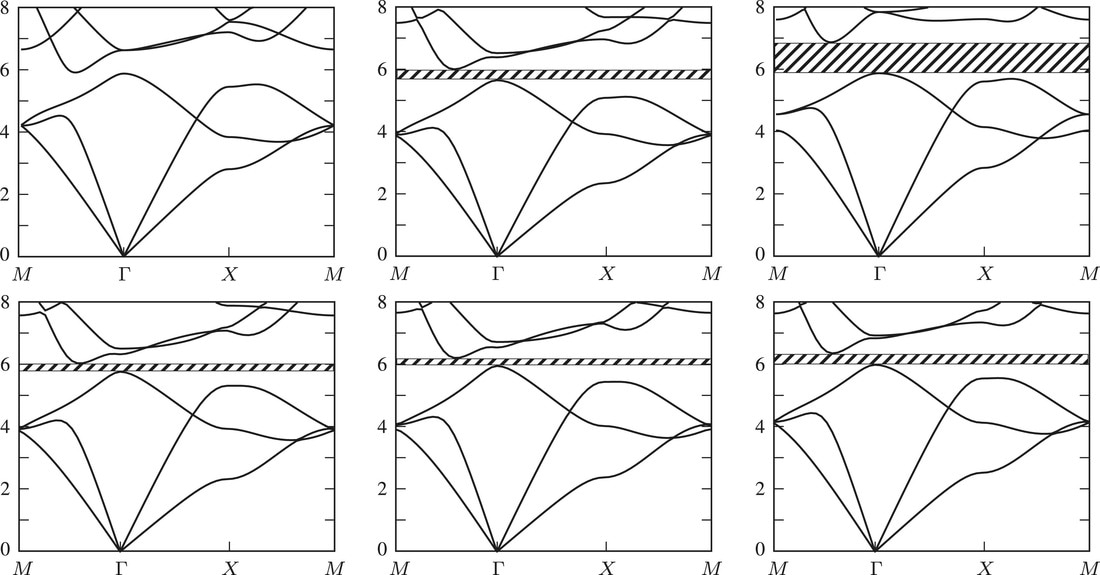
The second paper, focused on the in-plane compressional/in-plane shear problem appeared in Extreme Mechanics Letters in early 2017. The figure below illustrates the mechanism of deforming the annular region in order to tune the band gaps. Band diagrams are shown for a number of different materials. The top left figure is a stress free solid with inclusions of radius R=r=0.275, the top middle is a pre-stressed annular region of Levinson–Burgess strain energy function type whereas the top right is a stress free solid with inclusion size R=0.36. The bottom three diagrams are 3 different compressible Mooney–Rivlin materials with (from left to right) S1=1, S1=0.8 and S1=0.6. All of the pre-stressed materials have initial radius R=0.3, axial stretch ζ=1.4 and volume change . Stop bands are indicated by the shaded regions. As well as introducing this new configuration of potentially tunable phononic crystals, these papers also illustrated the extension of the Plane Wave Expansion (PWE) technique of determining band gaps to the case where material properties can vary continuously (periodically) in space, rather than simply being piecewise constant as is traditionally the case.
|
|